Экспериментальное исследование методов и приемов систематизации и обобщения знаний учащихся при изучении темы «Алгебраические уравнения» в 9 классе

Тест

Действительные числа

1. Обратить обыкновенную дробь в десятичную:

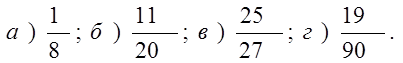
Ответ: а) 1) 0,102; 2) 0,125; 3) 0,1205.

б) 1) 0,55; 2)0,505; 3)0,255.

в) 1) 0,(925); 2) 0,9(25); 3) 0,92(5).

г) 1) 0;21; 2) 0,2(1); 3)0,(21).

2. Обратить десятичную дробь в обыкновенную:

а) 0,15; б) 0,225; в) 0,(6); г) 2,2(41).

Ответ: а) 1) 3/20; 2) 4/17; 3) 3/5.

б) 1) 9/40; 2) 2/19; 3) 1/40.

в) 1) 2/3; 2) 1/9; 3) 3/7.

г) 1) 2219/90; 2) 2219/990; 3)2219/999.

3)Выписать из данных чисел иррациональные:

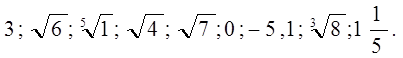
Ответ: а) 1)

2)

3)

4. При каких х имеет смысл выражение:

А.

Ответ: а) 1) х>0; 2) x<0; 3) x- любые числа.

б) 1) х>5; 2) x<5; 3) x- любые числа.

в) 1) х ≥5; 2) x≤5; 3) x- любые числа.

Б.

Ответ: а) 1) х ≥0; 2) x≤0; 3) x- любые числа.

б) 1) х ≥3; 2) x≤3; 3) x- любые числа.

5* Упростить выражение:

Б.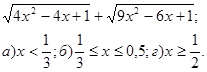

Ответ: а) 1) 2-5х; 2) 5х-2; 3) x;

б) 1) 5х-2; 2) 2-5х; 3) x;

в) 1) 2-5х; 2) x; 3) 5х-2;

В.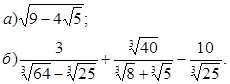

Ответ: а)

б)

Тест

Комплексные числа.

1. Изобразить комплексные числа на координатной оси: z1=4-6i; z2=3+i; z3=-5i; z4=4-0i; z5=-1,5=3i; z1=-2-8i;

2. Для комплексных чисел z1 и z2 найти:

1)z1+ z2; 2)z2- z1; 3) z1z2; 4) z1: z2:

z1 = 5-3i , z2 = -4+7i.

Ответ:1. а)z1+ z2=1+4i; б)z1+ z2 =4+i; в)z1+ z2=2+3i;

2. а)z2- z1=9-10i; б) z2- z1=-9+10i ; в)z2- z1= -9-10i ;

3. а)z1z2=-41+47i ; б) z1z2=-1-47i ; в)z1z2=1+47i ;

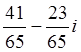4. а)z1: z2=; б) z1: z2=; в) z1: z2=.

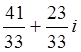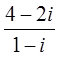3. Составить квадратное уравнение с действительными коэффициентами, если известен один из его корней

х1 =

Ответ: а) x2-6x+10=0; б) x2-6x+8=0; в) x2+6x-10=0

4. Вычислить: 1)i21 ,2) i75 ,3) i44

Ответ: 1) а)i; б)1; в)-i;

2) а)i; б)1; в)-i;

3) а)i; б)1; в)-i.

5. Выполнить действия:

1) (2+5i)2 (3-i);

2)*

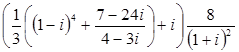
Ответ: 1. а)-43+81i; б)-83+81i;в)-23+39i;

2. а)8i; б)0; в)-4i.

План-конспект №1. Тема урока: «Графический способ решения систем уравнений».

Цели урока:

открыть совместно с учащимися новый способ решения систем уравнений, закрепить навыки построения графиков элементарных функций;

формировать потребность приобретения новых знаний, создать условия для систематизации (самосистематизации) усвоения умений и навыков;

развивать математическую речь при комментировании решения;

воспитывать уважение друг к другу, взаимопонимание, уверенность в себе, развивать самостоятельность и творчество.

Ход урока.

Для урока мы используем следующую литературу: Учебник Ю.Н. Макарычева “Алгебра 9” под редакцией С.А. Теляковского., “Сборник задач для проведения письменного экзамена по алгебре за курс основной школы” “Дрофа” Москва 2001г., Материалы Единого Государственного Экзамена.

Во время урока учащийся ведет лист самосистематизации, где в ходе урока оценивает свое участие по 3-х бальной шкале (0,1,2).

1 – Самоопределение к деятельности. Организационный момент

Эпиграф: Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю (Гёте И.)

2 – Актуализация знаний и фиксация затруднений в деятельности.

Новое о педагогике:

Признаки проблемного обучения
Развитию творческой познавательной деятельности учащихся во многом способствует проблемное обучение. Иногда проблемное обучение противопоставляют сложившимся в теории и практике формам методам обучения, что является глубоко ошибочным. Проб ...

Сущность, цель и задачи процесса воспитания орфоэпической культуры младших школьников на уроках чтения
Речевая культура личности является одним из основополагающих компонентов общей культуры человека и требует постоянного совершенствования. В ее основе лежит существующее в сознании человека представление о «речевом идеале», образце, в соотв ...