Авторские образовательные технологии в обучении геометрии

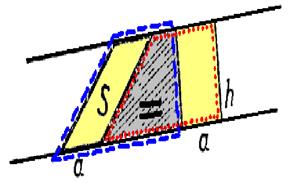
Рис. 2

Есть параллелограмм, площадь S которого надо найти. Рассмотрим пару каких либо параллельных сторон параллелограмма и будем считать их основаниями длины а. На прямой, содержащей одно из оснований, выбираем произвольную точку, из которой опустим перпендикуляр на прямую, содержащую другое основание. Отложив от этой точки отрезок длины а, из второго его конца опускаем такой же перпендикуляр. Этот перпендикуляр есть высота параллелограмма длины h.

Теперь рассмотрим два четырехугольника. На рисунке один из них обведен точечной линией, обозначающей красный цвет, а другой пунктирной – синий цвет. Соответственные стороны и углы этих четырехугольников равны, значит, равны и сами четырехугольники, и их площади. «Отрезав» общую их часть (штриховка), увидим, что площади оставшихся фигур равны (знак «=» на штриховке). Но от фигуры, обведенной пунктирной линией, останется параллелограмм, а от той, что выделена точками – прямоугольник с такими же основанием и высотой. Поскольку площадь прямоугольника ah, то и площадь параллелограмма S=ah.

Два последних абзаца содержат все то, что говорит учитель, а на рисунке – все то, что он изображает на доске. Этот рисунок и есть опорный сигнал доказательства. При этом нет привычных «Дано», «Доказать», нет никакой записи доказательства символами, только рисунок.

В.Ф. Шаталов рекомендует использовать обозначение геометрических фигур цветом и тогда речь уже идет не о трапеции АВСD или параллелограмме КLМР, а о «синей» фигуре и «красной» фигуре. Такой прием способствует быстрому охвату фигуры целиком, в отличие от обозначения фигуры буквами, соответствующими вершинам фигуры, при котором образ фигуры конструируется учеником из её составных элементов согласно обозначению.

На все это учитель тратить примерно полторы, максимум две минуты. Ученики в это время ничего не пишут, а только слушают, воспринимают, осмысливают рассуждение. Так как в нормальных условиях ученик способен без особых затруднений воспринимать рассказ учителя продолжительностью 15-17 минут, то на этом же уроке В.Ф. Шаталов предлагает вывести аналогичным образом и формулы площади треугольника, площади трапеции, произвольного многоугольника и др. Таким образом, менее чем за половину урока учитель изложит ученикам всю «теорию площадей», а на доске появится соответствующий данной теме ЛОС. Оставшуюся часть урока занимает многократное повторение и озвучивание ЛОС уже учениками. На следующем уроке ученики отчитываются по теоретическому материалу темы «Площади» письменным воспроизведением ЛОС по памяти его «озвучиванием» (у каждого из них имеется брошюра с ЛОС как дополнение к учебнику). Таким образом, все остальное время, выделенное на изучение этой темы, отводится на решение задач и многократное повторение теории.

Новое о педагогике:

Методы и прием логопедической работы по преодолению нарушений звукопроизношения у детей с дизартрией
Чтобы помочь детям овладеть правильным звукопроизношением, логопед должен иметь хорошую теоретическую и практическую подготовку. Ему необходимо владеть материалом, который составляет теоретическую основу знаний о звукопроизношении, знать, ...

Особенности организации контроля и оценки проектной деятельности школьников на примере создания сайтов
Выработка системы оценки проектных работ на уроках информатики требует предварительного ответа на следующие вопросы: предполагается ли включение самооценки участников проектных групп в общую оценку проекта? предполагается ли присуждение ме ...