Виды игр, их особенности. Краткие примеры

Игры усложняются за счет введения блок-схем с ветвлениями, а затем и с циклами. В конце изучения темы "Сложение и вычитание в пределах 10" учащиеся знакомятся с работой машины, функция которой является простейшим разветвленным алгоритмом. По схеме (рис. 7) учитель организует отработку устного счета.

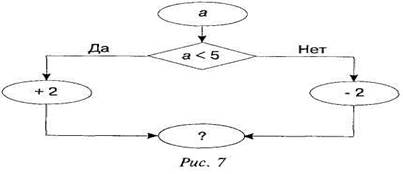
Данная блок-схема предоставляет новые возможности для умственного развития детей. Прежде всего, в деятельность учащихся явно включается оценочная компонента, которая вызвана необходимостью проверять выполнимость логического условия перед выбором следующего действия. Например, если на вход подано какое-то число а, то машина сначала проверяет, выполняется ли условие а < 5. Если условие выполняется, то машина прибавляет к данному числу число 2, а если нет, то вычитает число 2.

Новые умственные действия необходимы ученикам при решении обратной задачи (нахождение числа на входе машины по известному числу на выходе), когда учащиеся проводят анализ, убеждаясь в необходимости проверки своих решений: правильных ответов может быть один, несколько или ни одного.

Пусть, например, требуется установить, какое число следует подать на вход машины (см. рис. 7), чтобы на ее выходе получить:

а) число 7;

б) число 6.

Для числа 7 рассуждения учащихся будут примерно такими.

Число 7 на выход машины могло поступить по левой или по правой ветви. Если предположить, что число 7 получено по левой ветви, то перед блоком "+ 2" должно быть число, которое на 2 меньше, т. е. число 5 (7-2 = 5). Число 5 на блок "+ 2" могло прийти только после блока сравнения с числом 5. Поскольку условие 5 < 5 ложно, то после сравнения число должно идти по ветви "Нет". Получается, что число 5 не может попасть на блок "+ 2" после блока сравнения. Значит, число 7 на выход машины по левой ветви поступить не могло.

Если число 7 пришло на выход по правой ветви, то перед блоком "-2" было число, которое на 2 больше, т. е. число 9 (7 + 2 = 9). Число 9 на блок "- 2" поступило после блока сравнения. Так как неравенство 9 < 5 ложно, то число 9 должно идти дальше по ветви "Нет", как и требуется. На блок сравнения число 9 приходит с входа машины, значит, для получения на выходе машины числа 7 на ее вход нужно подать число 9.

Если на выходе машина выдала число 6, то, чтобы узнать возможные числа на входе, надо проанализировать обе возможности:

1) на выход машины число 6 пришло по левой ветви;

2) на выход машины число 6 пришло по правой ветви.

Если предположить, что число 6 на выход пришло по левой ветви, то оно было получено после увеличения некоторого числа на 2. В этом случае до увеличения, т. е. перед блоком "+ 2", было число, которое на 2 меньше, а именно число 4 (6 - 2 = 4). Число 4 пришло на блок "+ 2" после блока сравнения. Так как неравенство 4 < 5 верное, то после сравнения число 4 должно пойти по ветви "Да", т. е. на блок "+ 2", как и нужно. Так как на блок сравнения число поступает со входа машины, то на выходе машины число 6 будет получено при подаче на вход числа 4.

Если допустить, что число 6 пришло на выход машины по правой ветви, то перед блоком "- 2" было число, которое на 2 больше, т. е. число 8 (6 + 2 = 8). Число 8 на блок "- 2" пришло после блока сравнения с числом 5. Так как неравенство 8 < 5 ложное, то после блока сравнения число должно идти по ветви "Нет", как и нужно. Поэтому число 6 на выходе машины можно получить, если на вход подать число 8.

Таким образом, число 6 на выходе получается, если на вход подать число 4 или число 8, т. е. задание имеет два решения.

Можно рассмотреть эту же задачу для числа 1 на выходе машины — она не имеет решения.

Первоклассники также знакомятся с работой вычислительных машин, реализующих циклические алгоритмы.

Новое о педагогике:

Внедрение регионального компонента в школьное образование
Образовательный процесс рассматривается как сложное историческое и педагогическое явление, представляющее собой совокупность исторических, социальных, психологических, культурных явлений, как единство среды и обучаемого. Основы нормативной ...

Особенности восприятия мальчиков и девочек как социально-педагогическая проблема
Восприятие действительности как научная проблема имеет особое значение в педагогике и психологии как базовый процесс для всех других видов деятельности развития личности в целом. Притягательность проблемы подтверждают многочисленные исслед ...