Методические особенности изучения Теоремы Безу в 7-9 классах

Теорема 3.

Два многочлена принимают одинаковые значения при всех значениях х тогда и только тогда, когда при каждой степени х они имеют одинаковые коэффициенты.

Доказательство.

Это утверждение моментально следует из предыдущего: если многочлены принимают одинаковые значения при всех значениях х, то они принимают одинаковые значения при числе значений, большем наибольшей из их степеней.

Организация обучения.

Так как на изучение теоремы Безу отводится мало времени, то следует определенным образом организовать изучение материала, то есть параметризировать учебный процесс.

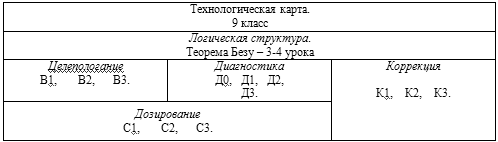
В педагогической технологии академика В.М. Монахова выделяются пять параметров: целеполагание, диагностика, дозирование, логическая структура, коррекция.

На этапе целеполагание выделим основные цели которые будут поставлены перед учащимся и сформулируем их в форме: " знать…", " уметь…", "понимать…", " иметь представление о…" (подробнее см. в технологической карте).

На этапе диагностика с помощью небольших самостоятельных работ (на 5-10 минут), получаем информацию о достижения микроцели или о недостижения микроцели, а также выявляются типичные ошибки учащихся (подробнее см. в технологической карте).

На этапе дозированиЕ определяем объем и содержание самостоятельной внеаудиторной деятельности учащихся (подробнее см. в технологической карте).

На этане логическая структура по числу микроцелей выделим группы уроков

На этапе коррекция организуем специальную деятельность учащихся по ликвидации пробелов, выявленных на этапе диагностики (подробнее см. в технологической карте).

7 класс.

Целеполагание.

В1. Уметь применять схему Горнера для вычисления значений многочленов.

В2. Уметь применять схему Горнера для нахождения корней многочленов и

нахождения корней целых алгебраических уравнений.

В3. Знать формулировки теорем о целых и дробных корнях многочленов с целыми коэффициентами.

В4. Уметь находить целые и дробные корни многочленов и уравнений любых степеней с целыми коэффициентами.

Диагностика.

Д0. 1. Выполните действия. (Устно)

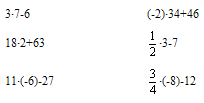
2. Найти сумму коэффициентов многочлена

а) f(x) = 3x4 + 2x3 + 15x2 – x – 1;

б) f(x) = 7x5 - 3x3 + 12x2 – 2x + 13.

3. Выпишите коэффициенты многочлена и свободный член.

а) f(x) = 3x4 + 2x3 + 15x2 – x – 1;

б) f(x) = 7x5 - 3x3 + 12x2 – 2x + 13.

Д1. Используя схему Горнера, вычислите значение f(x) = x4 + 3x3 + 2x2 + 1 при с=3; -4.

Д2. Определите, какие из чисел -5; 2 являются корнями уравнения x3 - 6x2 + 11x – 6 = 0.

Д3. Определите, какие из чисел 1, 2, -2, 4, 5, -13, 28, -7, 123, 3 не являются корнями многочлена:

а) x3 + 38x – 123;

б) 2x4 – 13x3 + 8x2 – 12x + 40.

Д4. Найдите рациональные корни многочлена:

6x5 – x4 + 2x3 - 2x2 - 4x – 1.

Коррекция.

К1. Затруднения в этой теме связаны с заполнением схемы Горнера (пропуск коэффициента).

Пример. f(x) = x4 + 3x3 + 2x2 + 1

Пути исправления.

1. Выпишите коэффициенты многочлена (при x5 , x4 , x3 , x2 , x) и свободный член.

f(x) = x5 + 4x3 - 53x2 + 25

2. Проверьте правильность заполнения первой строки схемы Горнера для многочлена:

f(x) = 7x5 - 3x3 + 12x2 – 2x + 13

3. Составить схему Горнера для многочлена f(x) =13x4 - 6x2 + x – 17

К2. Затруднения в этой теме связаны с заполнением схемы Горнера (арифметические ошибки).

Пути исправления.

1) Выполните действия.

2) Повторить правила выполнения действий с положительными и отрицательными числами.

Отдельным учащимся могут быть предложены индивидуальные карточки с вычислительными заданиями.

К3. Затруднения связанные с усвоением алгоритма нахождения значений по схеме Горнера.

Пути исправления.

1)Учащимся предлагается визуально оформленный алгоритм (см. ?)

2) При выполнении вычислений по схеме Горнера порядок действий указывается стрелками.

Новое о педагогике:

Патриотическое воспитание школьников как педагогическая проблема
В последнее время в России активизировалась работа по патриотическому и гражданскому воспитанию молодежи. Следует отметить, что это направление деятельности педагогов школ всегда было актуальным и важным, занимало ведущее положение, но еще ...

Характеристика общих методов воспитания
Главная функция методов формирования сознания — просвещение, формирование знаний в области социально-нравственных отношений, норм, правил поведения людей, формирование взглядов, ценностей. Основной инструмент, источник убеждения — слово, с ...